Questioning/posing problems
Having a questioning attitude; knowing what data are needed & developing questioning strategies to produce those data. Finding problems to solve.
Introduction
The Habits of Mind in my classroom are all closely interconnected, most important among them is Questioning and Posing Problems. This Habit underpins and serves as the impetus for the other mindsets. One challenge I have working with my students is their lack of engagement with the material. They learn what they need to and do the work that is expected of them, but they are often doing so at the surface level. This makes it much harder for them to learn math, and for me to teach them. My goal with teaching this Habit of Mind is that students will ask themselves questions in order to fill in gaps in knowledge, rather than wait for me to provide an answer. Students need to actively engage with understanding the interconnected world around them.
My students are too often turned off by challenges because they don’t want to be embarrassed by not knowing what to do. Practice with Questioning and Posing Problems helps prepare students to be more confident in new situations. This Habit helps students look for opportunities to connect what they do not know to more familiar topics. Exploring the “what-ifs” is critical. Entertaining hypothetical problems can reshape the way students consider their role in the classroom, but this does not come naturally in a rigid school system. My students are approaching the end of their high school careers and need to be prepared to tackle the nebulous demands of the non-academic world. Questioning and Posing Problems shows students that they are more than capable of doing so.
Table of Contents
Explicit Teaching
Thinking Critically
In this lesson, students were pushed to understand how prior knowledge applies to content they’ve never seen before through Questioning and Posing Problems. The goal was not to apply the past knowledge itself, but rather to demonstrate to students that learning intentionally can make new content easier to grasp. Students were using questions to make connections and see relationships between familiar content new content. It was hands-on; students were practicing and getting feedback on the questions they asked immediately.
This lesson speaks to the idea that math is interconnected, and that students’ learning in math truly is not discrete. Asking questions is what leads students to understand this themselves.
This is the simple slide deck I used to reference during the class discussion. The lack of detail makes room for students to ask insightful questions. The graphic on Slide 2 is what students asked questions about initially.
After students asked questions about the formula, I explained the difference between being critical and thinking critically. When being critical, students are making an emotional decision - usually out of frustration. I provided examples of what this could look like on the formula students were dealing with. Some of them pointed out that they asked similar questions. I took this opportunity to stimulate a class discussion about what a critical thinking question might look like when facing something new. I offered some examples to give students an idea of what is expected and restated the connection to exponential growth. With this context, students were asking more pointed and helpful questions. Below are some examples of students’ initial questions and questions that were posed during the discussion.
Initial Questions

These questions demonstrate that students were looking to complete an assignment. They were not seriously considering the implications and were asking questions with simple answers. Some of them could even be answered in the same graphic as the formula. As a baseline, these responses demonstrate the need for explicit teaching of this Habit of Mind.


These responses provide more room for discussion. Students are searching for explicit connections to prior content and asking if the same rules apply. Rather than asking what pieces of the formula are, they are asking why they are there and what they do mathematically. Students are taking a more intentional approach to learning this new formula and will be able to make deeper connections because of it. The fact that they ask these questions before I teach them the answers is integral to the learning process.
Teacher Reflection
This lesson was effective at starting a discussion about being inquisitive and putting our efforts in the right places. Students were surprised when I indirectly called them out for not putting forth the effort the work they do deserves. Even without referencing specific answers, some felt called out because they knew they could have done better. Providing an opportunity for students to improve their answers was vital to the lesson, and the results show that students were being more intentional about asking good questions. This provided the basis for building upon this Habit of Mind in other contexts.
Reinforcement Lesson #1
Content-based Reinforcement
In this lesson, students were working on reviewing and practicing the content they learned throughout the unit. It touched on the same content as the initial Questioning and Posing Problems lesson plan in addition to the new topics learned in the weeks since. This was a prime opportunity for students to reflect on and apply this Habit of Mind in content.
In this lesson, students worked in groups on a problem from one of the standards covered in the unit. They found the solution, but they were also responsible for teaching the problem to the class. As a part of this, students were prompted to anticipate questions from their audience. “What do you think a classmate will misunderstand about this problem?” Students were posing hypotheticals to themselves to prepare answers to potential misunderstandings in advance. The intention is that students are getting space to ask questions and becoming more comfortable questioning and being questioned.
Posing Problems
Students were given 10 minutes to work in their groups to create a short presentation that would teach the standard and address these prompts posted on the board. Implicit in the process of teaching is predicting and preparing answers for problems students will run into on the problems they are tasked with. A member of each group was responsible for writing down the issues they predict students may have.
As students considered potential problems that may arise during their mini-presentations, they wrote some notes for themselves. These students’ responses look relatively simple, and they don’t demonstrate the level of thinking that goes into anticipating errors classmates will make. During the planning phase, I pushed students to consider the breadth of errors students may make and how they can proactively address them. Questions asked during presentations reaffirmed the importance of Questioning and Posing Problems. Students were often surprised to hear someone in the class ask the exact question they expected them to ask. The fact that they considered them in advance made their presentations more effective.


These students are in different class periods, and they were given the same problem to present to the class. They didn't offer much depth in their notes, but they both gave effective presentations that addressed the hypotheticals they considered in the planning phase.
Internalization
My students are not used to writing responses about this kind of thinking, so there isn't the depth in their written responses that I would like just yet. In future activities like this one, I will focus more on having students discuss their answers to these prompts rather than use them to inform their presentation approach.Where my students have done really well is on the other side of this activity where they are responsible for asking questions for clarification. During the presentation of each groups’ solutions, the audience was tasked with poking holes in the presentation.
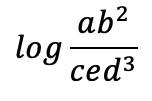
The question being discussed
This student’s questions were particularly effective at helping the presenter find errors in their explanation. This shows that students are starting to internalize and replicate some of the questioning techniques I use in the classroom and are asking high level hypothetical questions. This student in particular has modeled the questioning attitude my students are developing.
This lesson gave students an opportunity to practice asking content-related questions in a safe environment where they could get multiple forms of feedback. Students are internalizing my guidance and strategies for Habits of Mind in a classroom context. Personal growth on the part of the student is demonstrated through their ability to lead rigorous and engaging discussions about complex topics. Students are modeling my organization and inquisitive approach to learning math.
Reinforcement Lesson #2
Beyond the classroom
Teaching a Habit of Mind in a specific area of content all but guarantees that students will not apply the Habit in other areas. To counteract this, I chose to approach reinforcement in not only a new content area, but in a new way entirely. I want students to see this mindset as multidimensional. This lesson was adopted from a Curriculum for Community High School of Vermont Students which can be found here. Students were introduced to the SODAS method of problem solving, and used it to analyze problems not far removed from their own lives. For Questioning and Posing Problems, the SODAS Method provides structure that students can use to ask higher level questions and actively forge connections between problems.
On Slide 2, scenario A was modeled through a class discussion facilitated by me. Students provided answers to each step of the SODAS method, and I drew attention to the significance of what students were doing. Being able to identify and select a solution one can be confident in requires adequately exploring alternatives. Students then worked in their teams to work through Scenarios B and C. These questions connected to students' experiences outside the classroom, and they were better able to consider alternatives. They used their experiences to pose questions that gave them more tools to create solutions they could feel confident in.
Above are responses collected from students during this activity. Students were posing and considering problems in each of the scenarios to factor into their decision making. Students were tangling with hypothetical situations and pausing to consider alternatives. My students typically rush into decisions and look for easy ways to do things, but this activity slowed them down. They were asking for more information about each scenario and looking for ways to connect them to their lived experiences. I let them define the parameters of the solution; my only constraint is that they could justify their answers after fully considering their options.

I asked students to think about how they can portray what they learned, and I had a few students who were interested in making posters to represent the SODAS method. I really liked the poster this student made, as it shows that she was considering the importance of each step. The bullet points she included provide insight into how she has internalized the Questioning and Posing Problems Habit of Mind. She paraphrased and added to information I gave when presenting the SODAS activity, and I thought it would be helpful to share with other students. I hung it at the front of my room so that students are frequently seeing a reminder to slow down and consider what data might be missing.
Student Reflections
Written Reflections
In March, students reflected on various aspects of their personal growth. I have explicitly taught this Habit of Mind throughout the year, and students were asked to write about the extent to which they use Questioning and Posing Problems in their lives. Specifically, I was interested in seeing how my students have internalized this mindset and how it has impacted their study habits and education.
Student #3 highlights a significant impact of Questioning and Posing Problems. Beyond their ability to ponder hypothetical questions, this student recognizes their change in study habits. It was a major focus on mine throughout the year to push students to seek help. A major barrier to success in math is the mentality students take into learning it. Student #3 is representative of the classroom culture my guidance has created. My students are overcoming their math anxiety through this Habit of Mind and are making significant gains as a result.
Students #2 and #4 build on this style of growth by adding that they not only ask more questions, but better questions. Their inquisitive mindsets are bolstered by practicing this Habit of Mind. They are posing problems to themselves to better identify what they do not know and asking better questions as a result. They are better organized in their thinking and are developing study habits that prepare them for success outside of my classroom.
Evidence of Growth
As the district transferred to online, non-traditional instruction, students took on more responsibility for their own learning. As students practiced new topics, I included opportunities for them to reflect during the learning process. In this lesson, students answered simplifying rational expressions problems and self-graded their responses. Because I couldn't be there in person to guide them through feedback, students were responsible for understanding their mistakes on their own.

1. This student is not struggling with solving the equations, but they are having difficulty understanding the new concept of undefined value. They can ask for more specific help as a result.
2. This student is struggling with the new content and clearly needs to be retaught the material. Now, they know what to look for when they review notes and video lectures.
3. This student saw that their issue was not in understanding the concept of simplifying rational expressions, but in the process of solving. They know that they need to practice factoring.
First, students were asked to identify the errors they made. They could discuss gaps in their knowledge that led to the mistakes they made as they practice these problems. The important step here is that students were able to recognize where they made mistakes in their answers, rather than simply mark them wrong. The internal monologue students are having as they learn new content is a marker of their significant personal growth.
Students used this information to ask pointed questions to get the help that they need. They were able to pinpoint the help they needed and could either get help from me or from other resources on the internet. This skill has led to a successful transition to non-traditional instruction, as my students are more than capable of leading their own learning due to the study habits I taught throughout the school year.

1. This looks like a simple question that could be easily answered in class, but it gets to a deeper level of understanding mathematical thinking.
2. This student has identified the need to focus on factoring and is interested in better identifying common mistakes in factoring. Their question is more general, but I can point them to resources and practices that serve their particular needs.
3. This student is asking a specific question. At the beginning of the year, they would have simply gotten frustrated and given up. They know exactly where they need help and can get quick and effective feedback.
Conclusion
Students often see math as the subject with objectively correct answers. The world is not that simple, and, as an educator, I am intentional about breaking down students’ preconceptions about learning. There is a significant number of complex and interesting relationships students can explore in a math classroom. Some of the best learning comes from the hypothetical questions students pose during the learning process.
What I have seen in my classroom has been inspiring. Students are becoming fluent in some of these questioning strategies and anticipate the kinds of questions I will ask during instruction. They are identifying and combating common misunderstandings they themselves may have had initially. They ask themselves “What will Mr. Rolfes ‘misunderstand’ about my answer?” and preemptively provide the clarity that I expect when providing answer.